Copyright © 2024 Kirk Rader

Algorithmic Musical Composition

[This page concentrates primarily on analog synthesizer techniques. See For Dennis for a purely digital example.]

Go ahead. Press ⏵

After all, what's the worst that could happen?

What humans perceive as sound is the result of rapid changes in air pressure causing our ear drums to vibrate. So long as these vibrations occur within certain ranges of frequency and amplitude, the arrangement of tiny bones and sensory nerves within our inner ears transduce them into bioelectric signals sent to our brains, which process and interpret them as recognizable sounds.

Such changes in air pressure are conventionally visualized and described mathematically by analogy to ripples on a still body of water when something disturbs its surface. In this analogy, striking a drum's head is like tossing a pebble into a pond on a windless day. The mass of the stone displaces some amount of fluid as it passes through the water, causing a characteristic pattern of changes to the water's pressure. When those pressure changes reach the pond's surface, they appear as ripples emanating from the point at which the pebble entered the water. The ripples have a distinctive shape that is caused by the interplay of the size, shape and mass of the pebble, the density and viscosity of the water, the size and shape of the pond, and so on. The ripples are tallest when the pebble first enters the water, then become lower over time as the energy from the impact dissipates. Eventually the system returns to equilibrium. The water again has a smooth, motionless surface until the next pebble is thrown. If multiple pebbles are thrown when the ripples from previous pebbles have not yet died out, the pond's surface is covered by complex patterns of ripples, where the motion of one ripple might either reinforce or cancel out the motion of some other ripple.

In the case of sound waves caused by striking a drum, the drumstick or mallet is like the pebble, the drumhead is like the pond's surface. Striking the drum causes ripples on the surface of the drum. The size and shape of the ripples are determined by factors such as the elasticity of the drumhead and its taughtness. Other factors include the size and shape of the body of the drum, the physical characteristics of the object used to strike it, and so on. The height and shape of the ripples in the drumhead cause a corresponding pattern of changes to pressure in the surrounding air. The eardrums of anyone in hearing range then are induced to ripple in sympathy to the ripples in the drumhead due to those changes in air pressure. (Hence the antique term sympathetic vibrations as a way of describing how resonance works.) This is why sounds are described by acousticians and recording engineers using the terminology of sound waves and wave forms. Since any wave form can be depicted by graphing some mathematical function, it is common to visualize sound waves using such graphs and to describe them using mathematical terms like sine wave.

A recording of a sound stores a representation of the sound waves in a way such that they can be transduced into changes in air pressure via a speaker, which then enter our ears in the same fashion as the original sound. An analog recording represents a stored sound using a continuously varying physical property where each point in the "analog" of the sound directly matches the corresponding point in the original sound's wave form.

For example, a vinyl disk stores acoustical vibrations as physical textures on the sides of grooves cut into its surface. A turntable's playback needle vibrates as a result of brushing against that texture as the disk spins. The needle's vibrations are converted electromechanically into a continuously varying voltage. That voltage is passed through an amplifier and ultimately to the electroacoustic transducer in a speaker. The speaker's membrane vibrates according to the changes in voltage, which resonates through the air to listeners' ears as a reproduction of the original sound.

In the same way, an analog tape stores acoustic vibrations as patterns of intensity of a magnetic field imparted along its length. Rather than a physically vibrating needle, a tape machine's playback heads transduce these variations in the magnetic field to a continuously varying voltage. From that point on, the process is the same as that described for a turntable. That is why you can connect a turntable and tape player to a single amplifier, feeding a single set of speakers. Internally, the "sound" is really just an electrical current whose voltage varies over time in "sympathy" to the recorded sound waves, right up until it reaches the speakers, where they are converted back into actual sound waves.

[For completeness, a digital recording stores the record of the vibrations as a series of binary numbers which then undergoes digital to analog conversion (DAC) to become an audio signal conveyed as a varying voltage... but let's leave that aside for now since we are concentrating here on analog synthesis and playback.]

The point to understand for our present purposes is that whatever medium was used to store a sound, the playback device must be able to transduce the representation of the stored vibrations into continuous changes to an electric voltage. That voltage is ultimately sent to a speaker which converts the changes in voltage to movements of a diaphragm. The vibrating diaphragm causes corresponding rapid changes in air pressure. The result is that listeners hear a reproduction of the original sound in the same manner as if they had been present when it was being recorded, though with a cumulative loss of fidelity resulting from the physical characteristics of the intermediate transducers and storage media, governed by basic laws of nature involving constraints like friction, inertia, and entropy.

The process by which such recordings are created is the same, but operating in reverse. A microphone consists of a membrane which vibrates in resonance to changes in air pressure, just like a person's eardrums vibrate in resonance to sound waves. The microphone transduces those vibrations into -- you guessed it! -- a continuously varying electric voltage. That electric signal is fed into a device which stores the changes in voltage as changes to whatever recording medium is in use: vibrations in the cutting needle for a vinyl disk template, changes in intensity of electromagnets in the recording head of a tape machine, etc.

I.e. to create a recording, a sound is first transformed into a continuously varying voltage which is then used to create some physical analog of the original sound waves. To play the recording back, the stored analog of the original sound is again transformed into a voltage:

Analog synthesizers are electronic devices for directly creating audio signals as continuously varying voltages, suitable for use with audio recording devices, but where no "real world" source of acoustical vibrations was involved.

Any time a term like signal. signal path, audio or audio path are used in the context of music synthesis, it refers to the continuously varying voltage representing the analog of an acoustical vibration. This is to be distinguished from control voltage (CV) or control path, discussed later.

Elementary Psychoacoustics

A number of characteristics of sound vibrations combine to form a given sound's timbre: the subjective experience of the sound that allows us, for example, to distinguish between different musical instruments playing a given note, or tell the difference betweeen one person's voice and another's. Such characterisics include:

• The wave form (or "shape") of the vibrations.

• The frequency (or "pitch") of the vibrations.

• A vibration's envelope (how the amplitude and wave form change over time).

The terminology of "frequency" and "amplitude" are best explained by reference to extremely simple wave forms, like sine, rectangle, sawtooth etc. Such wave forms are easy to visualize and describe mathematically but rarely occur naturally in anything close to their pure forms.

Consider the following three tracks displayed in an audio editing program:

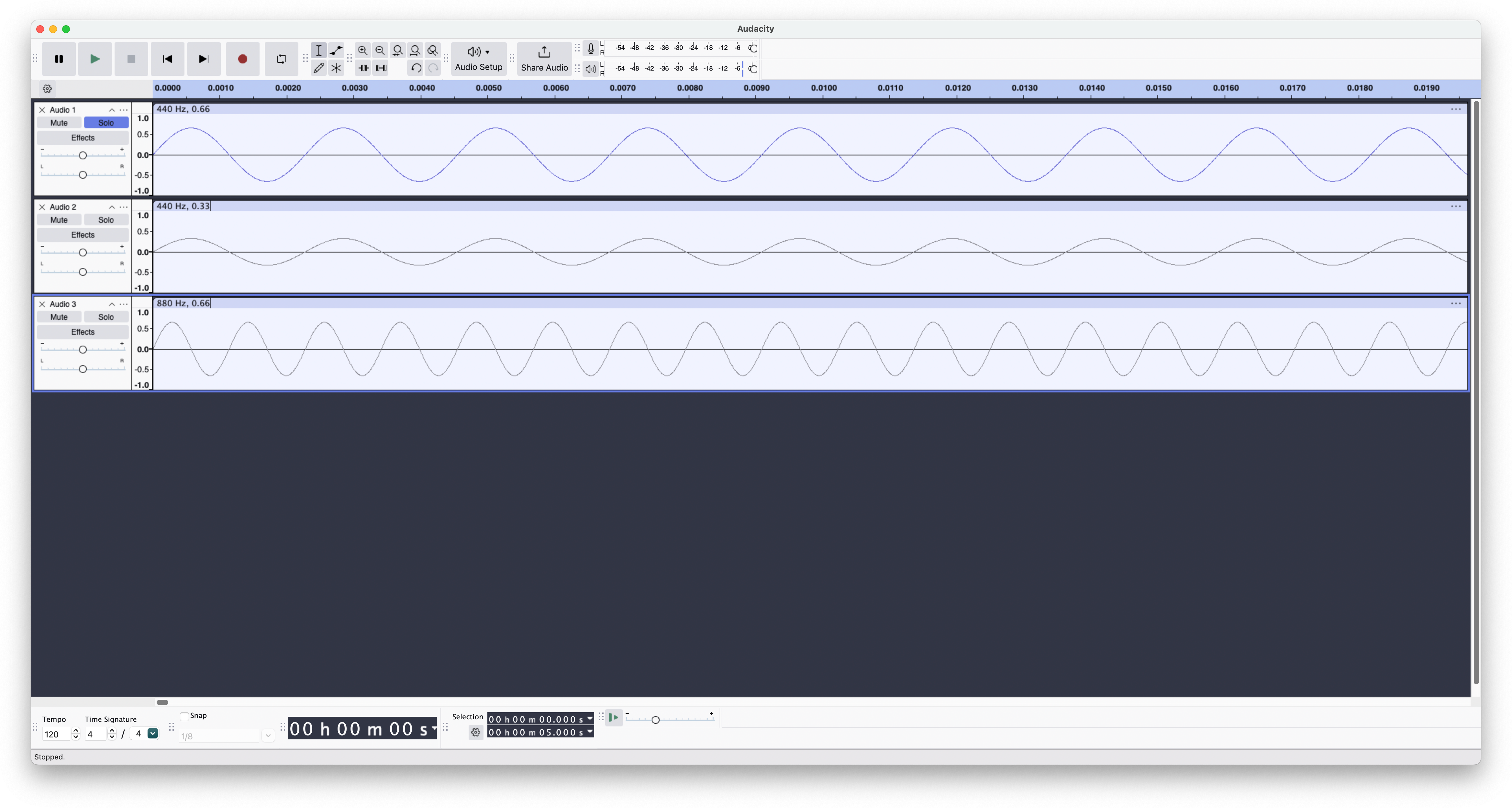
The top track contains a 440 Hz sine wave at a particular amplitude (440 Hz corresponds to "concert A," the pitch used by players in an orchestra so that their instruments will all be "in tune" when played together). Here is what that track sounds like when played on its own:

440 Hz Sine Wave

This is called a "sine wave" because the wave's shape can be exactly represented by graphing the mathematical sine function:

$$v=a\sin (pt)$$

where $t$ is a point in time, $p$ and $a$ are scaling factors representing the tone's pitch and amplitude, respectively, and $v$ the audio signal's voltage at that time.

The term "440 Hz" refers to the fact that this particular sine wave repeats at 440 Hertz, i.e. it traverses one cycle (from zero volts, to peak, to valley and back to zero) 440 times each second.

The second track is the same 440 Hz sine wave, but at half the amplitude. I.e. it is again a 440 Hz sine wave, but the distance, top to bottom, between the higest and lowest points in each cycle is half of the corresponding distance in the preceding track. This results in a tone that sounds exactly the same as the first one, but at a noticeably lower volume:

Softer 440 Hz Sine Wave

The third track is a 880 Hz sine wave, at the same amplitude as the first. The result is a tone that is the same volume as the first one, but an octave higher in pitch:

880 Hz Sine Wave

Visually, note that the peaks and valleys line up from left to right in the first two tracks, while the peaks and valleys in the third track are closer together, i.e. the peaks and valleys occur more frequently as one progresses through time in the third track compared to the first two. Thus, the third track represents a higher-frequency wave. Humans perceive higher frequencies as higher pitches and larger amplitudes as being louder. The keys on a "tempered" instrument like a piano or organ each correspond to a particular pitch in conventional musical notation. For example, striking the A key immediately above middle C causes a properly tuned piano's corresponding string to vibrate at 440 Hz, the frequency of the first two of the preceding sine waves.

Now consider this screen shot from the same audio editing software:

The track depicted contains a sawtooth wave at the same frequency and amplitude as the first sine wave, above. It sounds like this:

440 Hz Sawtooth Wave

It is perceived as being the same pitch as the 440 Hz sine wave. It has a noticeably different quality to its sound, however, as if it were being played by a different musical instrument -- e.g. like the difference between a flute and oboe. Human hearing is such that differently shaped waves are perceived as sounding distinctively different from one another, even at the same pitch and amplitude. Note also that even though the sawtooth wave has the same overall amplitude when graphed as the first sine wave, above, it actually sounds a bit louder when played back. This is due to the presence of overtones, discussed later.

The essence of electronic musical composition is finding creative ways to put all of the preceding principles together.

Wave Forms As Musical Notes

Composite Wave Forms (Fundamentals vs Overtones)

Any naturally occuring sound will have a fairly complex wave form that can be understood using the mathematics of signal processing to be the sum of a particular set of sine waves, each at a specific frequency and amplitude. A sufficiently chaotic jumble of sine waves at different frequencies and amplitudes sounds like noise, e.g. the hiss of steam escaping a radiator or the sound coming from the speakers of an old analog TV that is not tuned to any station. A truly random distribution of frequencies across the full range of audible frequenices is referred to as "white" noise, by analogy to the colors in the visible light spectrum:

White Noise

Noise that contains a preponderance of frequencies lower in the audible "spectrum" is referred to as "pink" or "red," again by analogy to light colors. White light that is passed through a filter than only allows lower frequencies to pass through becomes pink or red depending on the filter's cut-off frequency. By analogy, "white" noise that is passed through a low-pass filter will sound "redder":

Red Noise

Here is what the preceding two wave forms look like in an audio editing program:

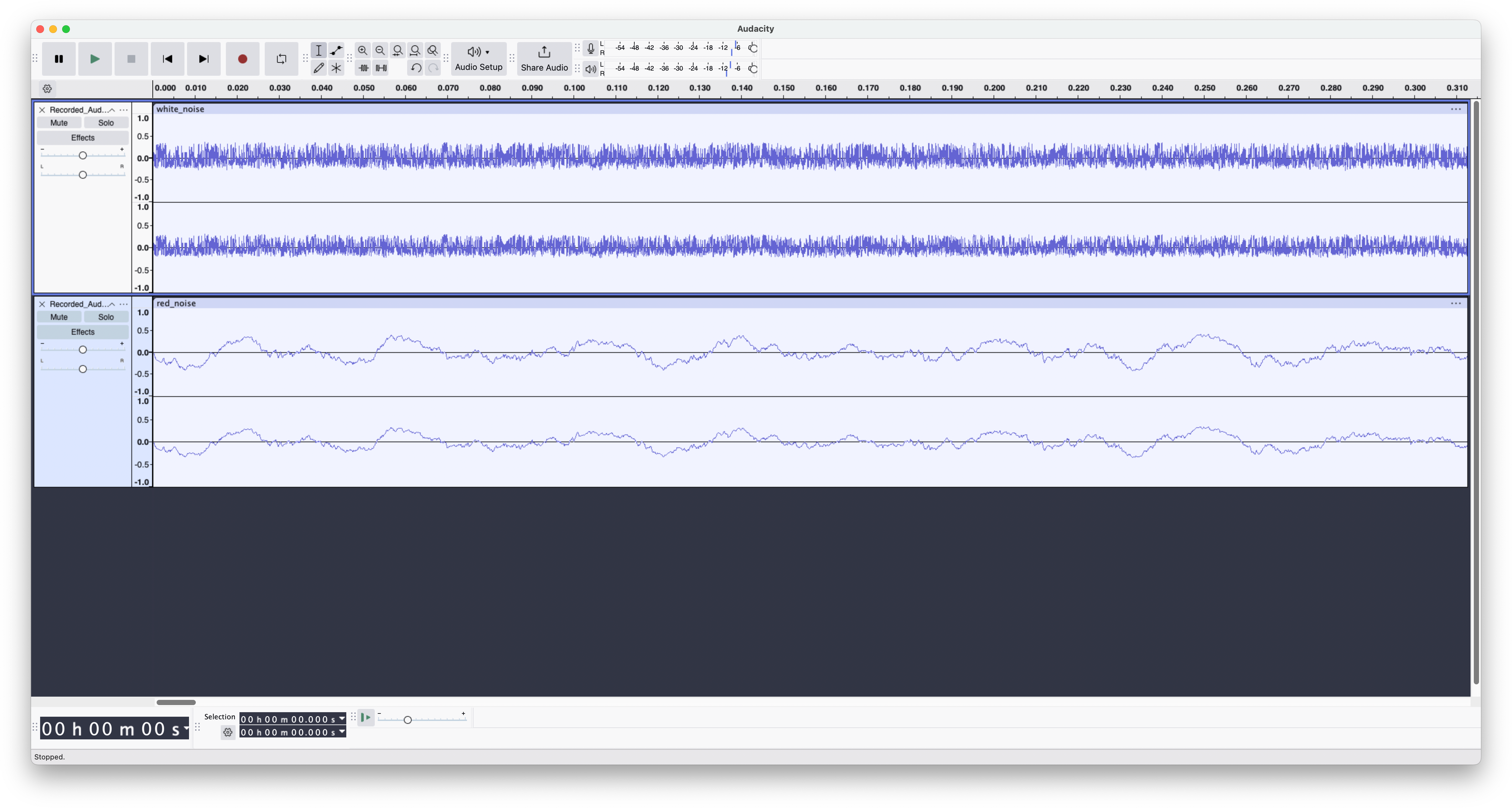
Note that the preceding sound wave graphs both consist of a randomly varying signal voltage with the same overall amplitude. The white noise graph varies faster over time than the graph of red noise, because it contains more frequencies in any given span of time. Because the white noise contains more frequencies per unit of time, it sounds louder than the red noise for the same reason that the sawtooth wave, above, sounds louder than the corresponding sine wave. Even though noise is not particuarly "musical" on its own (it is, after all, called "noise" for a reason) it does find its way into many analog synthesizer setups for a variety of purposes, as will be seen later.

In order to sound "musical," the sine waves comprising a given "note" must conform to certain rules. The loudest (highest amplitude) sine wave should be the lowest audible frequency present in the sound wave. That is called the fundamental frequency and will be the note's perceived pitch. Additional sine waves at perceptible frequencies and amplitudes should occur at frequencies with specific mathematical relationships to the fundamental frequency. Such additional frequencies are called overtones. One of the things that makes a violin sound different from a flute and a flute, in turn, different from a trumpet is the distinctive patterns of overtones at specific amplitudes present in the sounds they emit. A sine wave consists of nothing but its fundamental, while any other wave form consists of a fundamental plus some number of overtones. White noise sounds louder than red noise, and a sawtooth wave sounds louder than a sine wave because, in each case, the former represents a greater transfer of energy from sound waves to ear drums compared to the latter in the form of changes in air pressure due to the inclusion of more frequencies per unit of time.

Dynamic Properties of Musical Notes

As a consequence of the physical properties of whatever is producing a sound -- vocal chords buzzing, sticks or mallets striking drum heads, bows scraping across strings, etc. -- a sound's wave form and overall amplitude will change over time in various ways. Consider what happens when a stick strikes a drum.

First, the stick imparts energy to the drumhead at the point at which it lands. How much energy is determined by the stick's mass and velocity as determined by Newton's laws of motion. The energy absorbed by the drumhead causes waves to run through it similar to the ripples on the surface of a pond caused by tossing a stone. Those ripples are tallest when the stick first strikes, but quickly die out as their energy dissipates throughout the material of which the drumhead is made. We hear a short burst of sound, as these very short-lived waves resonant to our eardrums through the air.

A bowed string instrument works very differently, even though it is subject to the same laws of physics as a drum. The friction between the bow and the string causes the string to vibrate at a frequency that is determined by a combination of factors including the string's elasticity, length and taughtness. The strength of the vibrations -- i.e. the amplitude of the wave form it produces -- are determined by the amount of energy imparted by the bow, which is affected by the speed at which it is moving and the amount of pressure applied. Again thanks to classical physics, the string's own inertia means that it takes a bit of time for the vibrations to emanate from the point at which the bow makes contact and reach maximum amplitude along its entire length. This causes a small but noticeable "ramping up" of the volume of the note when the bow is first applied. But as long as the bow keeps moving against it, the string keeps receiving energy and so keeps vibrating. Because of the lower mass and air resistance at each point on a string compared to an extended surface like a drumhead, a string's vibrations take longer to die out after the bow is removed, unless they are mechanically surpressed. (The latter is how string players achieve staccato: they keep the bow pressed against the string to damp its vibrations more quickly than when they end a note by removing the bow from the string entirely.)

And so on for plucked string instruments, brass and woodwinds. The materials of which they are constructed and the manner in which they generate sound are, on the one hand, all governed by the same simple laws of physics but with results that sound different due to each instrument's particular mechanical properties. Among the factors that give each instrument its own unique timbre is the rate at which their amplitude ramps up and dies out and the way their sound waves' shapes changes over time as a note is played. These changes of a note's sound over time is called envelope.

For the purposes of understanding how musical sounds are perceived, it turns out that envelope can be broken down into four distinct phases:

Phase	Description
Attack	The time from which energy is first applied to when it reaches its maximum
Decay	The time from when energy has reeached its maximum to when it reaches the level at which it is sustained
Sustain	The amount of energy continously applied while a note is being played
Release	The time it takes for the energy to die out after it is no longer being sustained

Drums, for example, have nearly instantaneous attack and very short decay. I.e. they are at their loudest almost from the instant at which their sounds first start, and their loudness tapers off just as quickly. Depending on various physcal characteristcs, such as the differences between the construction and operation of a snare drum and a cymbal or piano, a percussion instrument might or might not have any appreciable release -- the time it takes for the sound to die out completely after its initial decay. Drum heads' vibrations damp out to below audible amplitude nearly as fast as they begin when struck, while a piano's strings can "ring on" for quite some time if allowed to do so by use of the sustain pedal. Either way, the defining characteristic of a percussion instrument is that it has no true sustain (despite the name of a piano's pedal). By comparison, human voices as well as wind and bowed instruments can have appreciable sustain levels, determined by the breath control of the performers or the lengths of their bows.

That said, bowed and wind instruments can have a noticeable "ramp up" in amplitude during their attack phase compared to plucked or percussion instruments, because it takes a little bit of time for sufficient energy to be transferred to the full length of a given instrument's strings or air column, depending on the mechanical properties of the means by which that energy is imparted to begin with.

This pattern of attack - decay - sustain - release (ADSR) forming a sound's envelope applies to a sound's wave form as well as its amplitude. The perceptible difference between the timbres of a woodwind and brass instrument, for example, has a lot to do with differences in their wave forms' envelopes even though their amplitude envelopes are quite similar. This is due to the difference between how their sounds are initially produced. A woodwind's wave form is relatively constant, even as its amplitude varies, while a brass instrument's wave form varies considerably from the attack / decay phases through the sustain / release phases due to the physical characteristics of human lips vibrating against each other while pressed to a mouthpiece compared to the far less elastic media of reeds and wooden or metallic edges while air is blown against them.

Old-School Modular Analog Synthesis

In order to produce wave forms with similar musical characteristics and complexities to those produced by "acoustic" instruments, the modules comprising a modular analog synthesizer are individual electronic components that generate or modify an audio signal represented as a continuously varying voltage. By chaining together a number of such modules in a single audio path, a huge variety of wave forms can be produced from a few basic building blocks. Since modular synthesizers have traditionally used patch cords to implement such chains of modules, a given configuration of modules to produce a particular audio output is referred to as a patch.

A typical patch might consist of:

• One or more oscillators, which generate audio signals in the form of some periodic wave form, e.g. sine, triangle, sawtooth or rectangular waves.

• One or more filters, which allow some audio frequencies to pass through unchanged, while attenuating (reducing the amplitude) of other frequencies.

• An amplifier, which modifies the signal's gain, i.e. the audio wave form's overall amplitude.

• ...and so on for more exotic types of modules such as envelope generators, ring modulators, sample and hold units etc.

Each type of module accepts input and / or produces output audio signals. It must also provide controls to set parameters for its operation. For example, an oscillator may have a physical knob for selecting the wave form to generate and another knob or slider to control the frequency of its output. In addition, most modules accept control voltages that can be used to vary such parameters dynamically as part of an overall patch.

These capabilities together enable a number of approaches to produce wave forms with more interesting acoustical complexity than simple sine, sawtooth, etc. waves:

• Additive synthesis uses multiple oscillators to create a fundamental together with a series of overtones directly.

• Subtractive synthesis passes an already complex wave form through one or more filters set to attenuate particular ranges of frequencies while passing other frequencies through without attenuation (or, optionally, boosting the amplitude of certain frequencies).

• Frequency modulation (FM) synthesis feeds one or more audio-frequency signals into another as control voltages.

FM synthesis is particularly useful with traditional analog synthesizers that have a relatively small number of oscilattors, each producing relatively simple wave forms. Such wave forms combine through FM synthesis chaotically, which produces a lot of acoustically interesting complexity from relatively few individual oscillators.

Some producers and performers are primarily interested in electronic instruments as a means of simulating traditional instrumentation at lower cost than hiring an orchestra's worth of musicians. Non-modular, typically digital, instruments are a better choice when all you want are buttons clearly labeled "piano," "strings," "horns" etc.

Electronic Music, as a meta-genre, is focused on musical techniques, timbres, and forms that simply are not possible using conventional instruments. Modular analog synthesizers are ideal for such pursuits.

Using Control Voltages

Traditional Musical Techniques

A low frequency oscillator (LFO) is simply a VCO (voltage controlled oscillator) which is configured to emit a frequency well below that which is perceptible to human hearing. Such a LFO is often used for traditional musical techniques involving changes to pitch, like vibrato, or tempo, like rubato.

For example, here is the audio output of a VCO emitting a sine wave at a given base pitch, with another sine wave emitted by a LFO patched into the VCO's CV controlling the former's frequency:

Vibrato

The result is that the VCO's output continously increases and decreases in pitch, producing vibrato from a patch like:

Uniquely Electronic Techniques

As with other aspects of electronic musical composition, analog modular synthesizers allow far greater scope for defining musical techniques than is possible with traditional instruments. For a very basic example, here is the output of the same patch as the preceding one, but with a far larger CV amplitude. The range of frequencies in the resulting "vibrato" is far beyond what a human could achieve with a traditional instrument:

Way Beyond "Vibrato"

And here is an extremely simple example of what is npossible using FM synthsis. Like the preceding example, it is the output of a VCO emitting a sine wave. In this case, however, the first VCO's frequency is being modulated by feeding the output of a second sine wave, whose base frequency is tuned to the same frequency as the source of the audio signal, into the first VCO's CV input controlling its frequency. I.e. the audio signal is the result of modulating a sine wave's frequency by another sine wave. If that were the end of it, there would be relatively little change to the output timbre because the two sines waves were tuned to the same initial frequency. However, for this patch, the second sine wave's frequency is itself being modulated by a third, low frequency sine wave, creating a continuously varying interference pattern between the first two VCO's frequencies:

Sine vs Sine vs Sine

On the one hand, the preceding sounds likes a continuously sustained note whose pitch is that of the constant fundamental frequency to which VCO 1 is tuned. Over time, however, the timbre changes continuously in a repeating pattern due to the overtones introduced by modulating VCO 1 using VCO 2 and varying VCO 2's frequency by way of the LFO. The speed of the sweep of changing overtones is determined by the frequency of the LFO.

As already discussed, a sound's envelope is an essential aspect of its timbre. An ADSR envelope generator is a type of module that emits a pattern of changes to a control voltage each time it is triggered by receipt of gate singals. "ADSR" is an acronym for Attack, Decary, Sustain, Release. An ADSR unit provides controls (e.g. knobs or sliders) to set values for each phase. In analog synthesizers, "acoustical energy" is represented in a patch as the value of a control voltage. Here is the same table as shown above, as it applies to the modules comprising a patch:

Envelope Phase	Description
Attack	Time it takes for CV to go from 0 to its maximum value when the gate "open" signal is received
Decay	Time it takes for CV to go from its maximum value to the sustain level
Sustain	Level at which CV remains after attack and decay phases, for as long as the gate remains "open"
Release	Time it takes for CV to go from its current level to 0 when the gate "close" signal is received

The gate signals are often provided by keyboard events: the gate "opens" when a key is pressed and "closes" when the key is released. However, other triggers can be used as the gate signals for ADSR. Many of the my compositions "play themselves" by using a single "clock" signal to drive both envelope generator and sample and hold units simultaneously, where a sample and hold unit emits a control voltage based on periodically "sampling" an input voltage and "holding" its output at that level until it is time for the next "sample."

To illustrate, consider a patch like:

The preceding will produce a sound like:

Smoothly ramping pitch

because the low-frequency sawtooth wave causes the frequency of the tone emitted by the VCO to continuously increase from its minimum value to its maximum value for each cycle of the control signal.

Adding a sample and hold (S&H) unit to the patch:

will cause the output to sound something like:

Stair stepping pitch

The output jumps directly from pitch to pitch instead of sliding continuously higher because the S&H unit sets its output voltage to whatever is present on its input each time the clock "ticks." The S&H unit holds its output at that level until the next "tick," when it again sets its output voltage to match its input at that instant in time. The smoothly ramping sawtooth wave is turned into a stair case. The width and height of the steps are determined by the relationship between the frequency and amplitude of the sampled voltage, the low-frequency sawtooth in this case, and the speed of the clock. For example, here is what the same patch sounds like sampling the same sawtooth but with the clock frequency sped up a bit:

Faster clock

Note that the output traverses the same range of pitches from lowest to highest in the same amount of time, as determined by the amplitude and frequency of the sawtooth wave emitted by the LFO in both of the two preceding examples. However, there are fewer, more widely spaced but larger jumps pitches in the first compared to the second because the faster clock results in a higher number of samples, each being held for a shorter amount of time, in each cycle of the sawtooth wave. If one were to increase the clock to a sufficiently high frequency, the output of the second of the preceding patches would eventually sound indistinguishable by human hearing from the first due to the same phenomenon of "anti-aliasing" that results from increasing the number of pixels used to capture a digital image.

But the same phenomenon works in reverse. Depending on the phase relationship between the frequency of the clock relative to that of the source being sampled, interesting patterns can emerge. Here is another recording of the same patch, but with the clock substantially slower than in the preceding two examples:

Phasing clock

The "ramping" pitches can still be discerned, but they start and end at different points in the "scale" for each cycle of the LFO sawtooth when the LFO and clock frequencies are not even multiples of one another. Layering multiple tracks created in this way can create interestingly complex rhythmic and harmonic patterns that vary continuously over time in a manner that is neither simply repetitive nor random.

To achieve a truly random "melody" is easy. Simply use a noise generator module as the CV input to a S&H unit:

Noisy melody

Example 01

It is obviously a matter of taste as to how "musical" any of the preceding examples sound.

Here is a composition that combines all of the preceding principles, using a Behringer 2600 semi-modular synthesizer, to produce polyrhytmuc music with harmonic and timbral structures not achievable using conventional instruments:

Example 01

Example 01 consists of three tracks of a couple of minutes each, recorded with VCO 1's Fine Tune slider set to the extreme right, middle and extreme left, respectively.

Example 02

Example 02>

Example 03

Example 03

Meloday Patch

Toms Patch

Unlike the preceding examples, the notes' values and timings are controlled by MIDI events sent by the following Ruby code, executed by Sonic Pi:

# Copyright 2024 Kirk Rader

# Example 03

use_random_seed 10
use_random_source :white

terminate = false

# master clock
in_thread do
  with_bpm 120 do
    midi (hz_to_midi 440)
    sleep 10
    180.times do
      cue :master
      sleep 1
    end
  ensure
    terminate = true
    cue :master
    sleep 1
    midi_all_notes_off
  end
end

# track 1 (low toms hard)
comment do
  in_thread do
    with_bpm 120 do
      beats = (spread 2, 5).rotate(2)
      loop do
        sync :master
        stop if terminate
        tick
        midi 36 if beats.look
      end
    ensure
      midi 36
      sleep 1
    end
  end
end

# track 2 (low toms soft)
comment do
  in_thread do
    with_bpm 120 do
      beats = (spread 2, 5).rotate(2)
      loop do
        sync :master
        stop if terminate
        tick
        midi 36 if !beats.look
      end
    end
  end
end

# track 3 (high toms hard)
comment do
  in_thread do
    with_bpm 120 do
      beats = (spread 3, 7).rotate(1)
      loop do
        sync :master
        stop if terminate
        tick
        midi 48 if beats.look
      end
    end
  end
end

# track 4 (high toms soft)
comment do
  in_thread do
    with_bpm 120 do
      beats = (spread 3, 7).rotate(1)
      loop do
        sync :master
        stop if terminate
        tick
        midi 48 if !beats.look
      end
    end
  end
end

# track 5 (bass)
comment do
  in_thread do
    with_bpm 120 do
      notes = (range 20, 31).shuffle
      loop do
        sync :master
        stop if terminate
        tick
        midi notes.look
      end
    ensure
      midi 20
      sleep 1
    end
  end
end

# track 6 (baritone)
uncomment do
  in_thread do
    with_bpm 120 do
      notes = (range 37, 48).shuffle
      loop do
        sync :master
        stop if terminate
        tick
        midi notes.look
      end
    ensure
      midi 48
      sleep 1
    end
  end
end

Summary

Other than Example 03, which was created using a Ruby program executed by Sonic Pi, you might be asking yourself, "wasn't this whole page supposed to be about algorithmic componsition? Where are all the algorithms?"

The answer, of course, is "the patches are the algorithms."

It is worth noting that not one of the examples on this page involved the use of a keyboard nor any other manual input device. I.e. none of them were "played" in the conventional sense. The Sonic Pi program sent commands to the synthesizer as MIDI events, in the same way that a MIDI keyboard or sequencer would send them, but the timing and note values of those MIDI events were entirely determined by the execution of the Ruby program shown above. For the other examples, any rhythms, dynamics or other time-based aspects were the result of the "logic" of how various wave forms combined along both the audio and control paths of a given patch. (Most of these examples, as well as my published works, are composites of multiple tracks arranged manually using digital audio workstation (DAW) software. Individually, however, most such tracks in my body of work were created in this entirely algorithmic fashion.)

But that is neither particularly radical nor "inartistic." A traditional musical score is an algorithm, expressed in the language of traditional muscial notation. Such algorithms are intended to be executed by the human performers who play the music encoded by the given score. Such algorithms are, however, more like recipes in a cookbook than like mathematical formulas. I.e. the choice of each and every "ingredient" and how they are combined in a conventional musical score is the result of a conscious decision by its composer, resulting from that particular person's whims and tastes at the time of composition, limited by the physical characteristics of the particular instruments listed in the arrangement and reasonable expectations of the performance capabilities of human musicians.

Similarly, the source code that was used to drive Example 03 is an algorithm expressed in the Ruby programming language, executed by a computer running Sonic Pi. I.e. the Ruby code is the musical score for Example 03 every bit as much, and in exactly the same way as a score written in musical notation. Though it looks nothing like music notation, each line was consciously and deliberately written by a person (your humble author) according to a particular set of transitory "artistic" impulses with the aim of achieving some particular esthetic result.

For the other examples on this page (and most of my published musical compositions), the algorithm is embodied directly in how the modules of various analog synthesizers are configured and patched together. They are algorithms that execute themselves. They represent music whose scores do not exist, even theoretically, independent of the physcial patches that produce their audible output. This is different from improvisation on conventional instruments, where the performer / composer could, themselves or else by way of an amanuensis, write down a score in conventional musical notation from memory or based on a recording.

That is the key concept which, in the late 1970's, simultaneously drew me toward this style of electronic music composition and toward computer programming as a career. I had already fallen in love with the sound of electronic music when I began studying symbolic logic and formal linguistics at UCLA in 1978 (including seminars on various topics in metamathematics conducted by Alonzo Church, himself.) At the same time, I started dabbling in the creation of my own electronic musical compositions. I was immediately struck by how the third of the following bullet points is a direct consequence (actually, a restatement in applied terms) of the first two foundational principles of computational logic:

• Any possible algorithm can be expressed as a formula of Church's λ-calculus.

• Any well-formed formula of the λ-calculus can be "embodied" as one of Turing's a-machines.

• Thus, any possible musical composition could, in principle, be embodied in an analog synthesizer patch given a sufficient number of the correct kinds of modules.^*

Another way of saying this is that just as the wave forms emitted by musical instruments can be described mathematically, so can all of the rhythmic and harmonic relationships that result from playing sequences of particular notes, for particular durations, at particular volumes. This is why there has always been such an affinity between mathematics and music. From this point of view, the modules comprising a patch can be understood as being mathematical functions which together form an arbitrarily complex recursive equation.

I never felt any great need to reproduce traditional musical sounds or forms by electronic means. (I occasionally do so, but usually only as experiments with particular tools or techniques, i.e. as "studies" for more purely electronic compositions.) Specifically, I consider traditional music notation and instrumentation more than sufficent for expressing traditional musical ideas. My passion as a composer is in exploring musical ideas which cannot be expressed or performed by traditional means. This is no less an "artistic" undertaking than composing and arranging more conventional music. It is just that the artistry occurs by way of experimenting with patches, recording the results, and layering the individual tracks in a final mix for any given piece.

Of course, I am far from the first to experiment in this way. Schoenberg famously experimented with randomness in his approach to "twelve tone" composition. Cage experimented with timbre in his compositions for "prepared" pianos. Modular synthsizers and similar tools allow this kind of experimentation to extend further and in directions not possible when restricted by the physical characteristics of traditional instruments and human players. The essential difference between the "West Coast" and "East Coast" movements in the development of electronic music is that the latter focused on integrating electronic music into ensembles which also included traditional instruments being played according to the rules of conventional musical forms while the former focused on the capabilities of electronic instruments to extend the range of musical possibilities.

---

^*Undecidable

The title and cover art of my first album, Undecidable (consisting of tracks I recorded in the late 1970's through the mid 1980's) are testaments to the conceptual origin of my musical style. Its "logo" is the following expression of the λ-calculus:

$$\begin{array}{rl}\text{Let }\mathrm{\Omega }& =\omega \omega \\ \text{where }\omega & =\lambda x.xx\end{array}$$

ω is a function which calls itself indefinitely, meaning that Ω will never receive any definite value within a finite amount of time. Such self-recursion resulting in an infinitely evolving outcome is analogous to using techniques like FM synthesis, which mix together elements between the audio and control paths of a patch to achieve complex sonic outputs from simple, mutually referential inputs.